Ok, I know I must be certifiably insane for taking it this far, but I just wanted to do this while its fresh in my mind and so that I have it documented for myself, and to visualize better what happens during say around 10ms.

check out the following diagram(available for limited time):



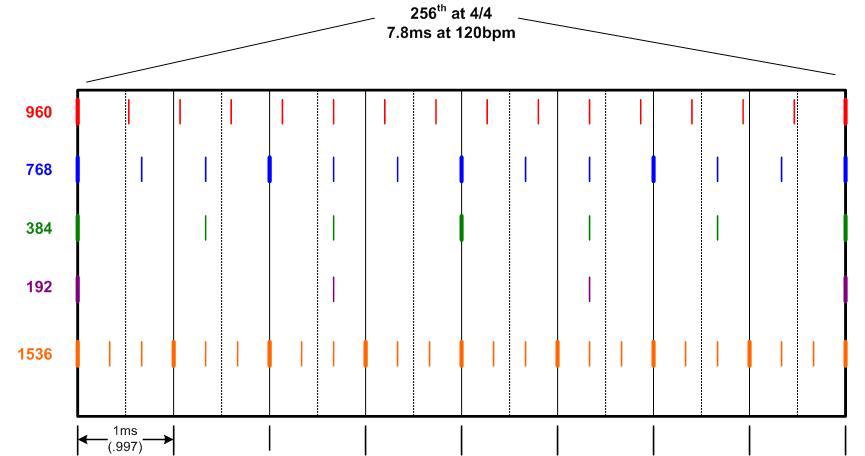
How to read this is that the big rectangle timeline represents one 256th note division of time, in 4/4 time at 120bpm, occurring over 7.8ms. The vertical lines in that big rectangle represent further metrical sub-divisions of a 256th note at 4/4, no triplets.

The tick marks along the bottom more or less show approximately 1ms of time. This value is not exact and depends on the tempo. Also the MM timer is not perfect. However, in Sonar, at some foggy interval of about 1ms, the MM timer goes off, obtains midi events from the hardware interface, assumes that they all happened at the end of that ~1ms time period and then assigns them to the closest red notch, which is the 960ppqn grid.

Notice that within the time that it takes for one 256th division, not a single one of those 960 ticks lines up on a metrical division. Only the ones lining up exactly on perfectly quantized 256th notes.

Now observe 768, 384, 192 and 1536. Not only do they have a lot of ticks that line up exactly on metrical divisions, but the ones that don't line up are actually evenly spaced as thirds in between the ones that do line up.

I don't really know what to make of all this other than to just say "interesting" and wonder what the effect would be if I could actually change the real midi resolution to some of these others. We are really talking about sub millisecond precision here in terms of where the resulting notes end up on the track.

We are NOT talking about capturing accurately. That is not possible no matter what. There is no way around the 1ms of midi slop due to the MM timer + whatever the DIN and USB is doing. However, when the notes finally do end up on the track, the question is, does it matter if they end up somewhat randomly scattered within a 10ms window, or will things sound tighter if the notes tend to gravitate towards metrical locations when they are stored?

Anyway, enough from me on this. Hope someone finds this interesting.

It's interesting, yes - but a little insane as well

What it made me think of, when Brundlefly pointed out the idea of quantization with less than 100% strength, means that all of the speculation about musical divisions and whatnot would be thrown right out the window, right?

I find it very interesting. Out of every x number of insane ideas comes one brilliant invention. Don't know if this is one or not, but your persistence is admirable and the chart is very pretty. One question that's difficult to ask/explain because it's hard to follow some of the logic and math. With real data, is the big rectangle fixed in relation to the verticle tick marks? IOW, if the rectangle is moved a few pixels to the left and the tick marks remain fixed in position, does that represent reality? The reason I ask is that, if that is so, then all the 768 and ticks would be consistently off the mark and then the highest resolutions (960 and 1536) would get us closest to real time.

How to read this is that the big rectangle timeline represents one 256th note division of time, in 4/4 time at 120bpm, occurring over 7.8ms

No big deal, but just to keep everything straight, 7.8 ms for 10 ticks at 960PPQ works out to 80 BPM. At 120 BPM, 10 ticks is only 5.2ms, and the max error caused by running at 960PPQ of half a tick is .26ms.

Yup. You're certifiable.

Edit: Oops. My mistake I was thinking the min whole number resolution of a 256th triplet. But the error is still only .26ms.

brunderfly:
There are 15 red ticks above. Try your math again... ;-) 15 ticks per 256th note at 960BPM. You are right that we are only talking about a sub-millisecond discrepancy. I have been saying that too. I have no idea if it makes any difference and nor do you. Anyone know of any scientific studies? I'm only observing it right now. Don't get your pants on fire, I still love Sonar. The other thing to remember is that most notes are held for a longer duration, at least 32nd's or much longer...so we are only really talking about a discrepancy of when the attack of the note starts and when the note ends. Oh but wait, that is a double discrepancy, because of each end of the note being represented by a separate midi event. (shrug)

dstrenz:
The ticks are fixed to the rectangle. Absolutely. PPQN ticks are ticks per quarter note. They are based on the meter. Period. Otherwise quantize operations would be meaningless. Every downbeat has the first tick of the beat and 960 more should follow, exactly on time until the next beat.

So the relationship between the colored PPQN ticks and the meter grid is absolutely the same every time. Or should be anyway. This only works out that they all start evenly on the front edge of the rectangle because 960,768,384, 192 and 1536ppqn all divide evenly into perfectly quantized 256th notes. On that rectangle, two vertical lines occur every 0.997ms at 120BPM. The ms reference is only to give people a general idea of the length of time we're talking about.

What can drift all over the place is the ~1ms window of when the MM timer will fire off and collect midi events to add to the track. Doesn't much matter though. All it means is that whenever midi events are being added, they are going to be originating from a ~1ms wide area, but they will always fall onto one of the red notches on the midi track. Actually as a sidenote, this diagram does help to visualize the 1ms slop incurred by using the MM timer.

Blades:
The issue with <100% quantization strength makes this issue perhaps even MORE relevant. Midi notes can only land on the red notches in Sonar. They can't be in between them ever. That is it. So let's say you want to quantize a note to 32nd, with 100% strength. It will pull the note's start time to a 32nd note boundary which will land exactly on a red tick mark that happens to also land exactly right on a 32nd note spot. If you use less than 100% strength, it will land on a different red tick mark, one that is not 100% metrically sound, but always one of the red tick marks.

dewdman,

What I was getting at with the "less than 100% quantize" was more in the region of normal musical values. For example, from your other chart in the other thread, at 960PPQN, 32nd notes would land at 120 tick intervals, so quantized to 100% strength for 32nd notes, would land you on these round numbers at musically relavent timings. If you said to quantize to 90%, you'd be 90% towards that tick from whatever "wrong" location the note was at, so lets say, for easy math, I was 10 ticks late (I landed at tick 130), 90% back towards 120 would be 9 ticks back in the quantized version instead of 10 if it were at 100%. Now, I'd be at tick 121, which probably isn't a musical value regardless of the PPQN - it's going to be about 1ms late (at tempo=120, right?) becasue I chose to quantize "loosely". this, of course, is just the absolute placement of the note - when it REALLY plays back is yet another question in terms of when I'll hear it, etc.

I guess I'm just yammering, thinking that the only time these resolutions really have any bearing is when you DON'T quantize, in which case you are trying to capture that ebb and flow of a real performance, which as we've all agreed, if played back reliably, would be "close enough", but with unstable stuff entering in we don't know if it's exact, if we'd notice the difference with HOW exact, and if we did, would we further notice a difference (at some sub understanding human level) as to whether it was a musically divisible location.

I get why you are asking the question, but the scientific end is going to get harder and harder to prove whether or not your experiment "works"...really it's a subjective thing.

If you could record two things and double blind test them with a bunch of us and ask which sounds more "right"...I think you'd find that we couldn't reliably tell which was which.

Carry on...

Regardless of whether you quantize or not, the notes all must land on the red 960 ticks. If you want the note on tick 121, because you used less than 100% of quantization..that is fine..it would not be exactly on a 32nd note boundary. But where it ends up being will not be in a metrically balanced location at finer level of meter detail.

I don't think I can explain this concept any better than I have already tried. If people still aren't getting it, then I give up. Do you get it? If you want the note to be slightly behind the beat by one tick, it can be one or two 960 ticks, which have no musical relevance whatsoever, or it can be a 768 or 1536 tick which would place the note in a location that has metrical balance in the sub-millisecond range. I'm not sold that its irrelevant that deep down.

capturing the fine nuance of a midi realtime performance is fundamentally flawed because of all the reasons we have discussed, but again, do you care if the notes end up on metrically balanced ticks or scattered non-musical random ones? You aren't controlling their exact location by your playing, the 960 grid is.

dewdman,

I feel like you think I don't get it. I get it. Maybe I just can't describe what I mean. I really don't want to do some of the math, so the example I gave was merely an example. Can you show me that the 90%, if given the exact situation that I described wouldn't be one of those "1/3 split" remaining items in the 768 time frame. If it does, then it's no more metrically accurate than 960. And in that case would be further away from the closest metrical subdivision.

So, at 960, for each 256th note of time, there are only 2 ticks that are on, one at the start and one at the end, where at 758, there are 5 that line up. So far, 768 "wins" for being more musical, but I feel like the scale gets tipped when I look at how much closer to the smaller subdivisions about half or more of the remaining ticks at 960 are - compared to the remaining, fewer ticks at 768 which are further from the metrical subdivisions. This is one of the areas that really would come down to a wierd answer when asking "which one has more accurate metrical breakdown?". If you happen to land on the even 768 ones or are quantizing, then fine, but if just recording freeform, it seems like there is likely a chance that you are going to be closer to metrical locations more often on average.

Some of it is theoretical, some may be subjective when it really comes down to it, but in this example with this model, it seems like there's not an actual answer.

Not trying to be argumentative here - since we're this deep into the unknown and possibly not usefully measureable, it's all conjecture.

I don't wish to debate with you Blade. Believe what you want. I'm only presenting the current situation that exists for whatever its worth. My diagram is accurate. Take that information and do whatever you want with it.

As I said some posts ago, there is no way for us to know either way without either (A) a way to try it out, which we don't have or (B) some scientific evidence about human perception in this area or on what top players actually do when they play, which we also don't have that information right now.

By the way 1536 is the resolution I am wishing for right now as an alternative to 960, though 768 is still interesting.

The interesting thing about 768, is that if Sonar provided it, you could quantize to 3 tick resolution, which would essentially force a type of 1024th division resolution with no out of time events... That is the same as using a 256ppqn sequencer with no "out-of-time" ticks. 1024ths, all exactly on meter boundaries is a good deal better for many people than 960, taking into consideration the midi slop eliminates the possibility for a musician to control absolutely where they want a midi event to land anyway.

960 can't represent 1024th divisions accurately that way, the best you can do to ensure no un-metrical events is to quantize to 15 ticks, which is the equivalent of a 96ppqn sequencer with no "out-of-time" ticks. 1536ppqn can actually represent 2048th divisions correctly with a 3 tick quantize and no out-of-time events, which is the equivalent of a 512ppqn sequencer that has no out-of-time ticks.

Also, the division by thirds that you mentioned is still more musical than the randomness and un-symmetricalness of 960.

This is all about tightening up the track and having options to do it metrically instead of somewhat randomly below a 256th division at 960.

Anyway, just observations...questions... Just explaining what I see and asking some unanswerable questions that should make all of us simply go "hmmmmm, I wonder". I don't see a need for you to discount what I'm saying. Nothing I have pointed out is actually debateble except for the question I still pose about whether a more musically metrical tick timebase would sound in some way tighter or more "musical"......a concept we are probably not ever going to find out the answer to. People have complained about timing and jitter and looseness and I am merely digging deep deep deep to try to find possible explanations.

Believe whatever you want that makes you happy.

Dewdman42,

If it counts for anything at all, I'll give you an A+ for tenacity.

Since I seriously doubt these issues will be solved (or even agreed upon) before I kick the bucket, if ever, I'm going to solve it for myself in a retro sorta way. I'm going to find a reliable old MCI JH24 to sync with my DTRS machines and retire the MS16. 48 tracks will do what I need just fine. Also, maybe I'll retire the music computer to internet only use just so I can keep up with the latest batch of bugs.

Carry on.